Alweer de derde versie van het artikel Onderzoekend en Ontwerpend Leren Ondersteund en Verrijkt door ICT. Ik schreef het vorig jaar al maar was het nog vergeten te plaatsen op mijn blog. Het is een verzameling geworden van verschillende inzichten.
Browsing Posts tagged Wetenschap & Technologie
Op 6 februari is er weer een W&T-academie in Utrecht! Je kunt je hier nog voor aanmelden! Meld je aan via de website!Ik ga er ook een workshop verzorgen over het programmeren van apparaten voor de bovenbouw van het basisonderwijs!
Afgelopen woensdag mocht ik op de W&T-academie een workshop verzorgen met de titel Programmeer de wereld om je heen. In een klein uurtje moesten de deelnemers een slagboom programmeren met behulp van de Makey Makey, Scratch en Lego WeDo. Het leuk om te zien hoe de deelnemers op verschillende manieren aan de slag gingen met de opdracht. Ook goed om te zien wat er nog aangepast moet worden voor een volgende keer.
Vandaag mocht ik voor de Vindplaatsscholen (scholen die vooruit lopen met Wetenschap en Technologie) kort iets komen vertellen over mijn onderzoek. Onderstaande presentatie heb ik hier voor gebruikt.
Lijkt het je ook leuk om mee te denken in mijn onderzoek? Dan ben je van harte uitgenodigd. Ik zoek nu leerkrachten die mee willen denken over de contexten die we leerlingen kunnen aanbieden. Ook ben ik op zoek naar scholen waar ik met leerlingen kan uitproberen wat ze allemaal al kunnen op gebied van het verklaren en ontwerpen van de technisch geprogrammeerde wereld.
Op woensdag 7 februari 2018 organiseert de Universiteit Utrecht de W&T Academie voor leerkrachten van basisscholen in regio Utrecht. De middag zal in het teken staan van onderzoekend en ontwerpend leren in de klas.
Psycholoog Stefan van der Stigchel houdt een lezing over zijn onderzoek naar aandacht en maakt daarna de vertaalslag naar de lespraktijk. In de workshops – die dit jaar zijn ingedeeld in ervaring met W&T – ga je samen met andere leerkrachten aan de slag met onderzoekend en ontwerpend leren. Tijdens de postersessie hoor je van andere scholen waar je rekening mee moet houden als je op school (verder) wil met wetenschap & technologie. Kortom; een prachtig programma met voor ieder wat wils!
Kijk voor meer informatie op de website: https://ktwt.nl/activiteiten/overzicht/wt-academie/, en meld je snel aan!
De afgelopen dagen heb ik nagedacht over hoe je computational thinking kunt integreren binnen een concreet project rondom onderzoekend leren. Daarbij wilde ik als uitgangspunt het artikel van Weintrop et al (2016) nemen dat een voorstel doet om computational thinking te integreren binnen science. Dit artikel richt zich niet zozeer op het basisonderwijs maar ik was benieuwd of ik hier een vertaling van zou kunnen maken naar het basisonderwijs. Ik zal mijn werkwijze en bevindingen in deze blogpost beschrijven.
Onderwerp voor het project
Als eerste heb ik een onderwerp voor het onderzoekend leren project gezocht. Ik heb hierbij de ideeën over crosscutting concepts als uitgangspunt genomen. Crosscutting concepts zijn concepten die binnen onderzoek een wezenlijke rol spelen. Paul Anderson zet deze concepten in een videoreeks op YouTube mooi op een rijtje:
- Patronen
- Oorzaak en gevolg
- Hoeveelheid en proportie
- Systemen
- Energie
- Structuur en functie
- Veranderingen
Bij elk crosscutting concept noemt Anderson voorbeelden waarmee je hier aandacht aan zou kunnen besteden. Zo noemt hij bij patronen bijvoorbeeld de seizoenen en bij oorzaak en gevolg als voorbeeld het groeien van planten. Voorbeelden die hij noemt zijn ook onderwerpen die je terugvindt in de kerndoelen van de SLO.
Seizoenen als onderwerp sprak mij aan. Hierbij kun je namelijk aandacht besteden aan patronen, oorzaak en gevolg, hoeveelheid en proportie, systemen, energie en verandering. Seizoenen als onderwerp an sich is natuurlijk nog erg breed.
Naast crosscutting concepts moet het onderwerp zich lenen voor de uitgangspunten zoals Weintrop et al (2016) die formuleren.
Dus het onderwerp zou zich moeten lenen om aandacht te besteden aan:
- data practices
- modelling and simulation practices
- computational solving problem practices
- system thinking practices
Bij het onderwerp dat ik kies moet dus data verzameld kunnen worden, moet er nagedacht kunnen worden aan de hand van modellen en simulaties, moet er probleemoplossend kunnen worden nagedacht en moeten systemen kunnen worden onderzocht.
Tot slot vind ik het belangrijk dat als ik aandacht besteed aan computational thinking het kinderen meer inzicht geeft in de wereld om hen heen.
Doorbordurend op het onderwerp seizoenen kwam ik uit op het onderwerp weer en specifiek daarbinnen het samenstellen van een weerbericht. Het dagelijks weerbericht biedt volgens mij mooie aanknopingspunten om met onderzoekend leren aan de slag te gaan en aandacht te besteden aan computational thinking zoals Weintrop et al dat formuleren. In het weerbericht maken meteorologen namelijk gebruik van allerlei weermodellen om het weer te voorspellen. Modellen die gezamenlijk enigszins een beeld geven van wat voor weer we kunnen verwachten. Een mooi voorbeeld waarin een weerman hierover iets uitlegt is te zien in onderstaande video:
Om me het onderwerp weersverwachting iets meer eigen te maken heb ik een artikel gelezen van Peter Lynch (2007) waarin hij schrijft over de ontwikkeling van het weerbericht en de rol die computers en computational thinking daarin spelen. Uit het artikel haal ik verschillende aspecten naar voren die van belang zijn voor het samenstellen van project rondom onderzoekend leren waarin computational thinking is verwerkt. Als eerste de zoektocht van de wetenschappers naar het gebruik van modellen die de weersveranderingen het beste in beeld brengen. En ten tweede de rekenkracht die nodig is om alle data die als input wordt gebruikt op tijd te verwerken.
Modellen
Bij de modellen gaat het om wiskundige vergelijkingen die uitdrukking geven aan verschillende aspecten die het weer en klimaat beïnvloeden. In het artikel worden verschillende modellen behandeld die elkaar opvolgen en elkaar beïnvloeden. Deze modellen maken gebruik van vergelijkingen die het basisschoolniveau ver te boven gaan. Voorbeelden hiervan zijn:
En zo worden in het artikel wel ruim 30 vergelijkingen genoemd die van belang zijn.
Het heeft naar mijn idee weinig zin om die modellen specifiek te behandelen omdat die niet aansluiten bij de beginsituatie van de leerlingen. Wat naar mijn idee wel zinvol is, is om leerlingen duidelijk te maken dat wetenschappers geprobeerd hebben om door middel van modellen het weer zo goed te voorspellen. En het is naar mijn idee ook zinvol om duidelijk te maken dat er niet één model is dat al het weer over de hele wereld kan voorspellen maar dat modellen met elkaar gecombineerd worden om tot een betrouwbare voorspelling te komen. Het is naar mijn idee ook zinvol om duidelijk te maken dat die modellen naar verschillende aspecten kijken van het weer: hoe lucht en water stromen, wat de luchtdruk is, hoe hoog de temperatuur, luchtdichtheid en vochtigheid is. En dat ze rekening moeten houden of lucht of land of over water stroomt. Ook vind ik het van belang dat leerlingen weten dat de atmosferische circulatie chaotisch is. En dat het dus weinig zin heeft om voorspellingen over de langere termijn te doen. Ander belangrijk aspect is dat die modellen niet vanuit het niets beginnen. Maar zich baseren op een uitgangspositie van het weer. Die uitgangspositie worden door waarnemingen van mensen en apparaten duidelijk gemaakt.
Rekenkracht
Om het weer te voorspellen is veel rekenkracht nodig. Lynch haalt in zijn artikel een wetenschapper, Richardson, aan die begin twintigste eeuw droomt over een weerverwachtingsfabriek. Om de atmosfeer bij te houden voor de weersvoorspelling, zegt Richardson, zouden zo’n 64.000 mensen nodig zijn. 64.000 mensen die alle data die binnenkomt verwerkt en doorgeeft zodat er uiteindelijk een weersvoorspelling uitkomt. Waarom is er zoveel rekenkracht nodig? Omdat de modellen starten met de waarnemingen. En om een betrouwbare uitgangspositie te krijgen moeten er veel waarnemingen worden gedaan. Waarnemingen op het land, op zee maar ook op verschillende hoogtes in de lucht. Waarnemingen op gebied van luchtdruk, windsnelheid, zonnekracht, luchtvochtigheid. Dat vraagt zoveel rekenkracht dat de eerste computer (de ENIAC) er 24 uur over deed om een weersvoorspelling te maken die precies 24 uur vooruit kon kijken.
Tegenwoordig zijn de supercomputers zo snel geworden dat de data binnen afzienbare tijd verwerkt is tot bruikbare weersverwachtingen.
Zo gebruikt de KNMI een supercomputer die een rekenkracht heeft van 58,2 terraflops. Dat wil zeggen 58,2 biljoen (een miljoen x een miljoen) berekeningen per seconde.
In het project zouden daarom ook deze stappen opgenomen moeten worden. Dus de realisatie dat het een keten is die er voor zorgt dat we een weersverwachting kunnen doen.
Het project zelf
Wat betekent dit voor het project zelf? In het project kun je aandacht besteden aan de modellen (of modelmatig werken) die wetenschappers gebruiken en de rekenkracht van de computers.
Fase 1 Confrontatie
In de confrontatiefase is het de bedoeling dat kinderen zich gaan verwonderen over het feit dat we weersvoorspellingen kunnen doen. Het weerbericht is zo’n alledaags verschijnsel dat dit waarschijnlijk eerst geproblematiseerd zou moeten worden: hoe kan een weerman nu weten wat voor weer het wordt? Glazen bollen waarmee je in de toekomst kunt kijken bestaan immers niet. En toch is dat wat een weerman doet: in de toekomst kijken. Hoe zou hij dat doen? Het bovenstaande filmpje over de weerman die verschillende weermodellen presenteert zou hierbij ook getoond kunnen worden.
Fase 2 Verkenning
In de tweede fase heb ik als mogelijke invullingen van onderzoekend leren op basis van Weintrop et al de volgende punten genoemd:
2a. Using computational models to understand a concept
4a. Investigating a complex system as a whole
4b. Understanding the relationships within a system
4c. Thinking in levels
2a. Using computational models to understand a concept
Er zijn mooie computational models over het weer maar die zijn lang niet allemaal geschikt om met basisschoolleerlingen te behandelen. Zo is er op de website BetaSimulaties een simulatie over wolken waarmee leerlingen aan de slag kunnen met academische modellen. SimSketch die ik een vorige blogpost noemde lijkt ook niet geschikt om met het onderwerp weer aan de slag te kunnen gaan. Die kan namelijk niets met lucht- en waterstromen, luchtdruk, temperatuur, luchtdichtheid en luchtvochtigheid. Een zoektocht op het web naar andere simulaties brengt me onder andere bij de animaties van de bibliotheek waar op een paar aspecten van het weer wordt ingegaan. Bijvoorbeeld hoe een regenboog ontstaat, schaduwen gedurende een dag en de waterkringloop. Het zijn leuke animaties maar ze leggen nog niet echt iets uit over het weer. Een verdere zoektocht brengt me bij CurriculumBits die een paar pagina’s hebben over aardrijkskunde. Hier wordt onder andere verschillende typen regen uitgelegd en depressies. Nadeel van deze animaties is dat je er zelf weinig invloed op uit kunt oefenen (variabelen kunt manipuleren). Nadeel is ook dat ze soms in het Engels zijn. Je zou leerlingen ook video’s kunnen laten zien van bijvoorbeeld SchoolTV maar ook daar is geen mogelijkheid tot manipuleren.
Een andere manier misschien om aan de slag te gaan met een computational model is door er een unplugged activiteit van te maken. Waarbij leerlingen zelf variabelen zijn die van invloed zijn op het weer. Klinkt leuk maar het idee van computational models is dat je iets met behulp van de computer kunt simuleren dat anders niet kan (geld, tijd of te gevaarlijk).
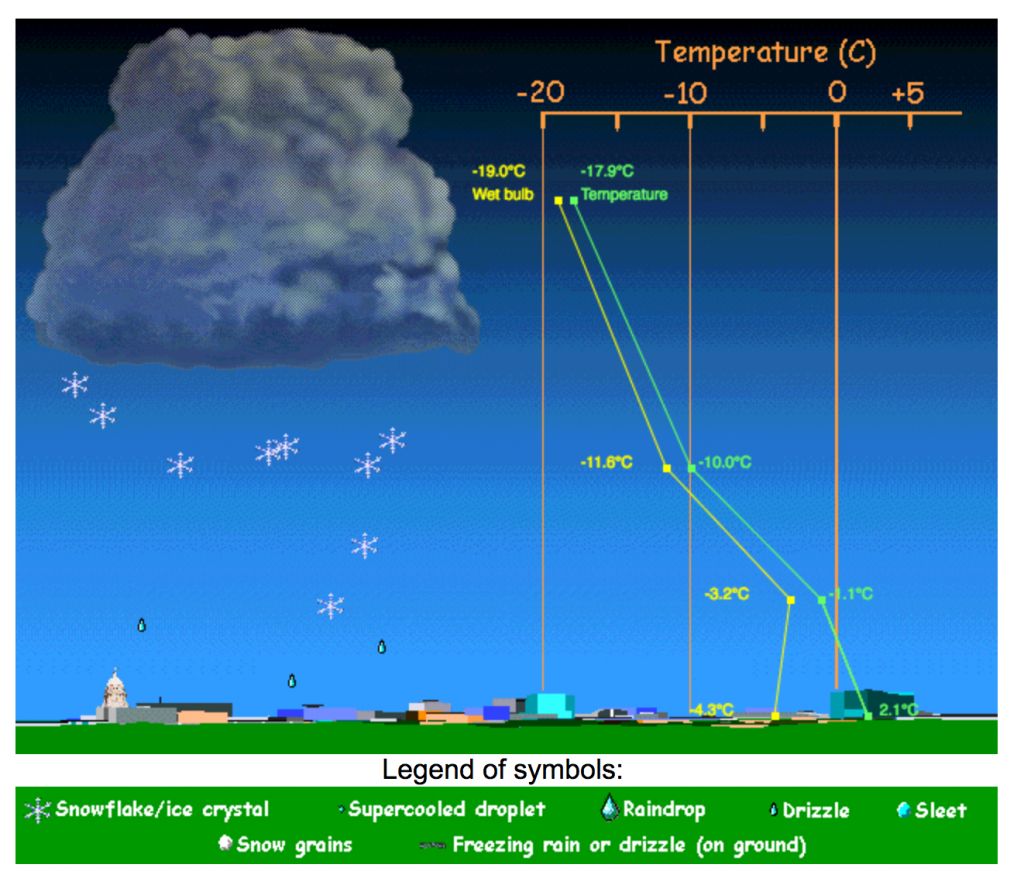
Computational models die wel geschikt zijn naar mijn idee zijn die van CIMSS (animaties).
Hiermee kun je bijvoorbeeld spelen met het type neerslag dat valt als je luchttemperatuur en de natteboltemperatuur verandert.
Wil dit effectief zijn dan moet je daar gerichte opdrachten bij geven en moeten leerlingen kennis hebben van de begrippen die hierin worden behandeld.
Kortom: Er zijn modellen waarmee je in stap 2 leerlingen aan het verkennen kunt zetten maar je moet daarbij goed opletten of die modellen ook dat doen wat je wilt bereiken. .
4a. Investigating a complex system as a whole
4b. Understanding the relationships within a system
4c. Thinking in levels
De bovenstaande stappen neem ik even samen aangezien die prima in samenhang uitgevoerd kunnen worden. Om een complex systeem zoals het weer te begrijpen en te verkennen bied je informatie aan (of laat je leerlingen die opzoeken) en doe je proefjes die de verschillende aspecten van het weer behandelen.
Fase 3 Opzetten experiment
Bij fase 3 heb ik verschillende aspecten genoemd die aan bod zouden kunnen komen bij onderzoekend leren. Ik behandel ze per domein. Als eerste de aspecten van modelling and simulation practices.
Modelling and simulation practices
De volgende punten noemde ik als voorbeeld die bij het opzetten van een experiment gedaan zouden kunnen worden:
2b. Using computational models to find and test solutions
2d. Designing computational models
2e. Constructing computational models
Bij het opzetten van een experiment gaat het om het bedenken en plannen van een experiment. Bij het bedenken van een experiment met behulp van een computational model (punt 2b) zoals dat over neerslagtypes kun je van te voren bedenken wat er zou gaan gebeuren als je variabelen op een bepaalde manier instelt. Het testen zou dan vallen onder fase 4 (uitvoeren van experiment) en je kunt daarna direct conclusies trekken (fase 5) en dat communiceren (fase 6).
Het zelf kunnen ontwerpen van een computational model en het bouwen lijken me op basis van het weer een te complexe opdracht. Je zou het met de leerlingen wel kunnen hebben over de keten die nodig is om te komen tot een weerverwachting. Daarmee heb je het naar mijn idee over decomposition. Een vaardigheid die veel genoemd wordt binnen computational thinking.
Computational problem solving practices
Aspecten van dit domein die geschikt zijn voor fase 3 zijn naar mijn idee:
3a. Preparing problems for computational solutions
3b. Computer programming
3c. Choosing effective computational tools
3d. Assessing different approaches/ solutions to a problem
3e. Developing modular computational solutions
3f Creating computational abstractions
Bij computational solutions denk ik aan de ondersteuning die de computer kan bieden om weerwaarnemingen van leerlingen te registreren en daarmee te rekenen. Bijvoorbeeld het gebruik van spreadsheetprogramma om de gemiddelde windsnelheid uit te laten rekenen. Als je dat wilt doen dan doorloop je stap a (hoe noteren we de gegevens in een spreadsheetprogramma), c, (welke tools is het meest effectief), b (het programmeren van functies in Excel (en die ook ook doorgronden)) en d (kunnen we dit ook nog op een andere manier berekenen). Hierbij kun je ook aandacht besteden (of stil staan bij) aan het feit hoe snel zo’n spreadsheetprogramma dit voor je kan uitrekenen. Veel sneller dan wij kunnen rekenen. Zeker als het aantal waarnemingen zo groot worden. Misschien kun je een wedstrijdje houden wie het snelst is: de computer of een snelle rekenleerling.
3e is naar mijn idee het beseffen dat je een probleem in stukjes kunt oplossen. Dus als het gaat om het weer dat je dan kunt kijken naar verschillende aspecten: wind, luchtdruk, etc. Punt f gaat volgens mij vooral op als je samen met de leerlingen het hebt over de manier van werken zoals je die hebt toegepast en kijkt of je die kunt toepassen op een ander aspect. In dit geval: we hebben Excel laten uitrekenen wat de gemiddelde windsnelheid is; zouden we dat ook kunnen doen voor de gemiddelde neerslag?
System thinking practices
Tot slot heb ik aan fase 3 het volgende toegevoegd:
4e. Defining systems and managing complexity
Dit gaat zeker op voor zo’n complex onderwerp als het weer. De vraag hierbij is: wat gaan we onderzoeken en tot op welke hoogte kunnen we hier antwoorden op vinden? Dit lijkt me vooral een rol voor de leerkracht die de kaders aangeeft.
Fase 4 Uitvoeren experiment
Onder fase 4 voegde ik de volgende stappen toe:
1a. Collecting Data
1b. Creating Data
3g. Troubleshooting and debugging
Stappen 1a en 1b. Dat lijkt me met het onderwerp weer/ weersverwachting niet moeilijk. Je kunt allerlei meetinstrumenten maken en gebruiken waarmee je data kunt verzamelen. Denk maar aan een thermometer, barometer en snelheidsmeter. Op een pagina van de SLO vind je hiervoor mooie voorbeelden. En als je weerinstrumenten zelf maakt dan kun je natuurlijk ook eerst kijken in hoeverre de instrumenten dezelfde gegevens opleveren. Dus hoe betrouwbaar zijn ze? En kunnen we ze ook betrouwbaarder maken?
Fase 5: Concluderen
Bij fase 5 heb ik de volgende aspecten toegevoegd:
1c. Manipulating Data
1d. Analyzing Data
Weerdata kan op verschillende manieren worden gemanipuleerd en geanalyseerd. Het ligt voor de hand om de data te koppelen aan kaarten of luchtfoto’s van de omgeving. Hoe nauwkeuriger de kaarten en/of foto’s hoe beter je de analyse kunt doen. Afhankelijk van je experiment kun je verschillende conclusies trekken. Bijvoorbeeld dat de windsnelheid op de ene plek groter is dan op de andere plek en de temperatuur hoger is op de ene plek dan op de andere plek.
Fase 6 Communiceren
Onder fase 6 voegde ik de volgende aspecten toe:
1e. Visualizing data
4d. Communicating information about a system
Ook dit lijkt me met het weerbericht goed te doen. Bijvoorbeeld door het maken van weerkaartjes (1e) en op basis daarvan een weerbericht maken (4d).
Fase 7: Verdiepen
Als mogelijkheid voor fase 7 noemde ik:
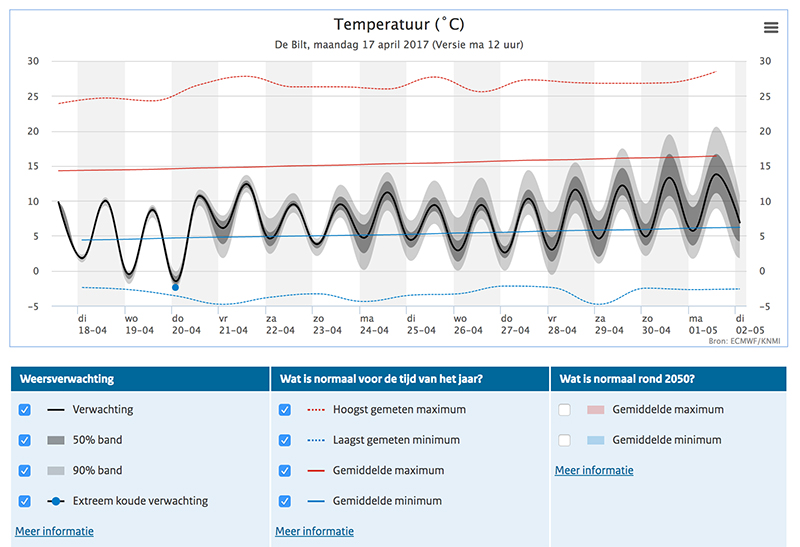
2c. Assessing computational models
Als het gaat over het weer en de weersverwachting kun je het hebben met de leerlingen over de betrouwbaarheid van de voorspellingen. Specifiek zou je het kunnen hebben over de weerpluim. Die laat zien dat naar mate de voorspelling verder in de toekomst ligt de onzekerheid toeneemt. Die onderzekerheid heeft te maken met feit dat de atmosfeer een chaotisch systeem is. Kleine invloeden kunnen grote gevolgen hebben.
Conclusie
Lukt het om voor een concreet onderwerp een onderzoekend leren project te beschrijven waarin de verschillende aspecten van computational thinking zoals geformuleerd door Weintrop et al zijn opgenomen? Antwoord: ja. Maar wel met een slag om de arm. De meeste onderdelen gaan prima. Maar Modelling and simulation practices is lastiger. Je bent daarbij als leerkracht vooral afhankelijk van bestaande modellen die je zou kunnen gebruiken. Modellen die recht doen aan de complexiteit van het onderwerp en tegelijkertijd zijn afgestemd om de doelgroep. Een niet eenvoudige opdracht. Ook niet onmogelijk trouwens. Want dit is precies van Pixar in a box doet.
De invulling van computational thinking zoals ik heb beschreven in dit artikel wijkt behoorlijk af van de manier waarop computational thinking normaal gesproken wordt ingevuld. De invulling zoals je die nu veel ziet is vooral gericht op verschillende aspecten die voortkomen uit programmeren. Dat is ook de manier waarop het IT-bedrijfsleven computational thinking propagandeert en waarvan de PO-raad zegt dat ze dit niet verplicht aan alle scholen wil opleggen. Ik ben benieuwd hoe anderen tegen deze invulling van computational thinking aankijken.
Tot slot
Voor de goede orde: ik heb ik dit artikel vooral gekeken naar de mogelijkheden van computational thinking binnen onderzoekend leren. De invulling van een onderzoekend leren project (rondom het weer) kan natuurlijk veel rijker zijn dan ik nu heb beschreven.
Ik heb in dit artikel ook nog geen specifieke groep benoemd waarvoor deze invulling van computational thinking geschikt is. Zelf denk ik aan een groep 8. Daarmee zou je ook direct na kunnen denken over de manier waarop deze invulling van computational thinking in de andere groepen vorm zou kunnen krijgen.
In mijn vorige blogpost vatte ik het artikel van Weintrop et al over Computational Thinking (CT) binnen Science en Math samen om een overzicht te krijgen hoe zij de verbinding zien tussen CT en deze vakgebieden. Ik concludeerde dat zij vooral Science als leidend uitgangspunt hebben genomen. Rekenen-wiskunde wordt vooral in de toepassingssfeer genoemd. Dat hoeft misschien niet altijd zo te zijn maar in dit artikel stond (naar mijn idee) science toch vooral centraal.
Ik gaf ook aan dat ik wilde kijken op welke manier er een vertaling gemaakt zou kunnen worden naar het basisonderwijs en dan specifiek naar rekenen-wiskunde en wetenschap en technologie (W&T). Ik wil met dat laatste beginnen. En dan van de W&T in eerste instantie de W, die ik kort door de bocht vertaal met onderzoekend leren. De vraag die ik daarbij vooral wil beantwoorden is:
Hoe kan CT zoals genoemd in het artikel van Weintrop et al ingebed worden in de cyclus van onderzoekend leren?
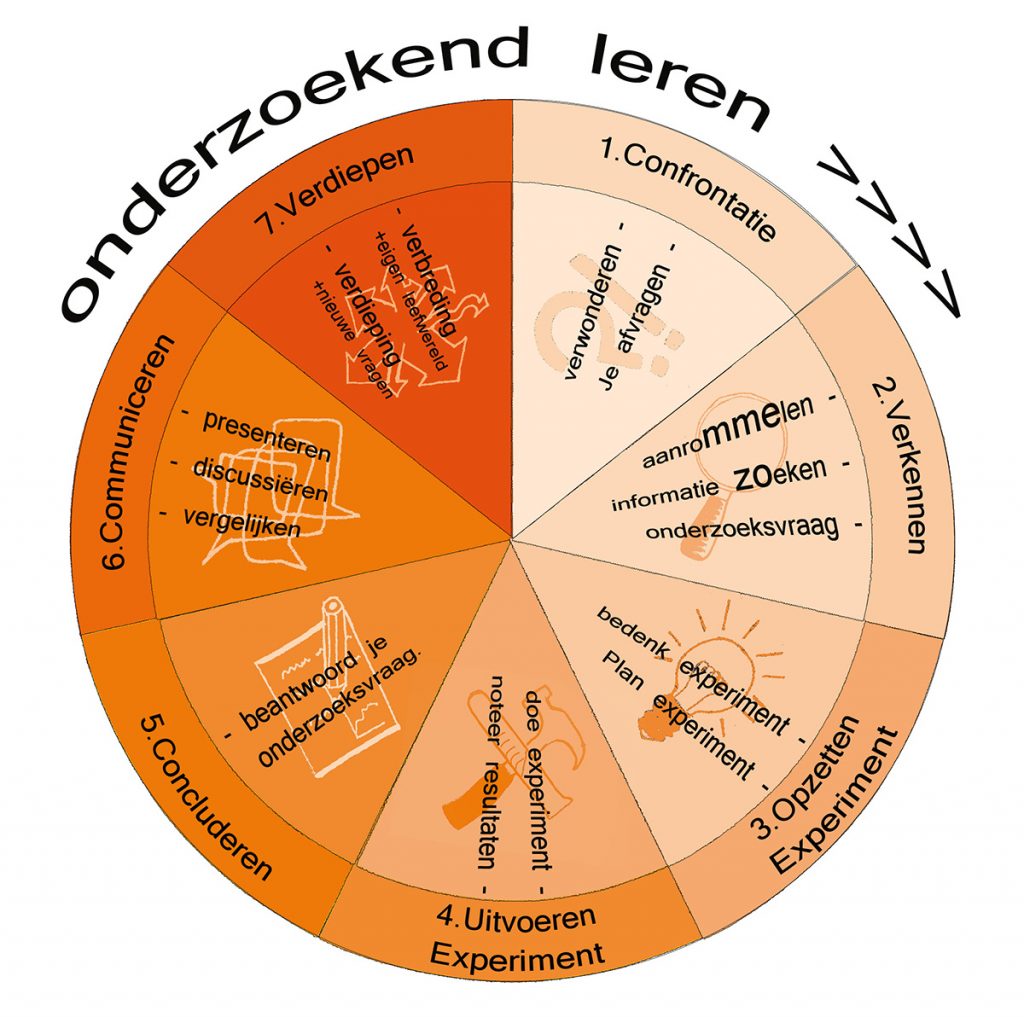
Cyclus van onderzoekend leren
Vooropgesteld dat onderzoekend leren meer inhoudt dan een cyclus en dat het al helemaal meer inhoudt dan het afwerken van een cyclus, wil ik kijken op welke manier de verschillende aspecten van CT gekoppeld kunnen worden aan de cyclus van onderzoekend leren. Ik gebruik hiervoor de cyclus zoals wij die op de HU Pabo aanbieden aan onze studenten. Dat is deze cyclus (afkomstig van Universiteit Utrecht):
1. Confrontatie.
In de fase van Confrontatie (verwonderen, afvragen) zie ik niet direct linken met de invulling van CT zoals Weintrop et al die geven. Ik zie die wel buiten dit model om, omdat de leefwereld van kinderen vol zit met computational practices. De publicatie van Hanno van Keulen, Wetenschap en Techniek, ijkpunten voor een domein in ontwikkeling, beschrijft de mogelijkheden van W&T in het dagelijks leven van kinderen. Deze zou gemakkelijk aangevuld, aangescherpt kunnen worden met CT.
2. Verkennen
In de fase van Verkennen zie ik verschillende mogelijkheden om met CT aan de slag te gaan. Mogelijkheden vanuit het model van Weintrop et al zijn naar mijn idee:
- 2a. Using computational models to understand a concept
- 4a. Investigating a complex system as a whole
- 4b. Understanding the relationships within a system
- 4c. Thinking in levels
Kinderen kunnen door middel van een computational model kennis maken met een bepaald concept. Met voorgeschreven opdrachten verkennen leerlingen dan dit concept. Kinderen kunnen kennis maken met verschillende systemen en proberen hier inzicht in te krijgen. Daarbij zouden gerichte opdrachten helpen om de relaties binnen een systeem duidelijk te maken en zouden ze uitgedaagd kunnen worden om de denken in verschillende niveaus.
3. Opzetten experiment
Bij het opzetten van een experiment (bedenken en plannen) zouden de volgende punten aan bod kunnen komen:
- 2b. Using computational models to find and test solutions
- 2d. Designing computational models
- 2e. Constructing computational models
- 3a. Preparing problems for computational solutions
- 3b. Computer programming
- 3c. Choosing effective computational tools
- 3d. Assessing different approaches/ solutions to a problem
- 3e. Developing modular computational solutions
- 3f Creating computational abstractions
- 4e. Defining systems and managing complexity
Het gaat bij alle punten om het voorbereiden van een experiment waarbij je bestaande tools gaat inzetten of zelf iets gaat maken. Het laatste punt (defining systems and managing complexity) gaat over de vraag, naar mijn idee, naar het afbakenen van je onderzoeksterrein.
4. Uitvoeren van het experiment
Bij het uitvoeren van het experiment (experiment doen en resulaten noteren) zouden de volgende punten aan bod kunnen komen:
- 1a. Collecting Data
- 1b. Creating Data
- 3g. Troubleshooting and debugging
Uit een experiment dat je doet komt namelijk data (in welke vorm dan ook) en kun je tegen problemen aanlopen die je moet oplossen.
5. Concluderen
Bij het onderdeel concluderen (beantwoord je onderzoeksvraag) zouden de volgende punten aan bod kunnen komen:
- 1c. Manipulating Data
- 1d. Analyzing Data
De data die je hebt gekregen uit je experiment moet je namelijk interpreteren. Daarvoor kan het noodzakelijk zijn om je data te manipuleren zodat je het gemakkelijker kunt analyseren.
6. Communiceren
Bij het onderdeel Communiceren (presenteren, discussiëren en vergelijken) zouden de volgende punten aan bod kunnen komen:
- 1e. Visualizing data
- 4d. Communicating information about a system
De data die je hebt genanalyseerd ga je tijdens de communicatiefase visualiseren zodat je ze kunt presenteren. Dat geldt ook voor punt 4d.
7. Verdiepen
Bij het onderdeel Verdiepen (verbreding, verdieping) het volgende punt kunnen passen:
- 2c. Assessing computational models
Als een soort discussie op je eigen onderzoek kun je terugkijken in hoeverre de gebruikte modellen iets zeggen over de werkelijkheid.
Conclusie
Naar mijn idee is het goed mogelijk om in de verschillende fasen van onderzoekend leren CT te integreren. Hoe dit er concreet in het basisonderwijs uit kan zien wil ik beschrijven in een volgende post. Ik kan me voorstellen dat niet alles aan bod hoeft te komen in één project. Ik kan me ook voorstellen dat in de onderbouw van het basisonderwijs de mogelijkheden beperkter zijn dan in de bovenbouw van het basisonderwijs. En ik kan me voorstellen dat leerlingen die meer ervaring hebben met onderzoekend leren of met CT weer meer aankunnen dan leerlingen die daar nog nooit mee gewerkt hebben.
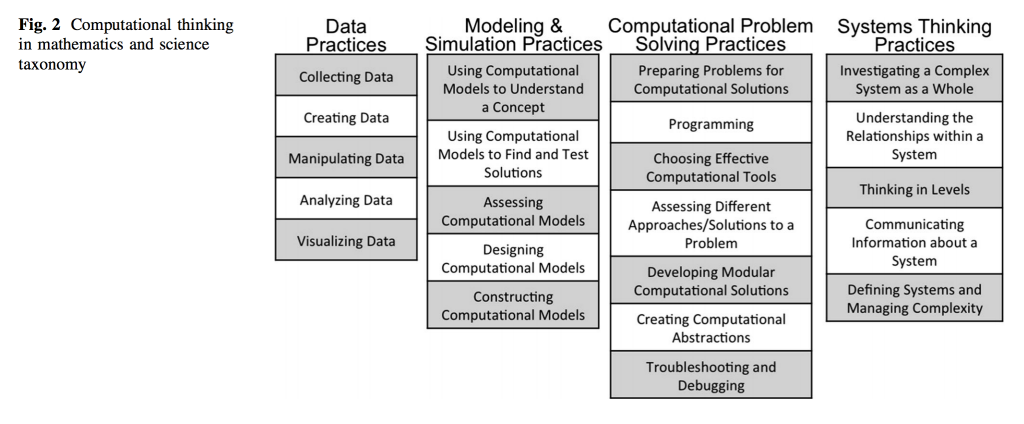
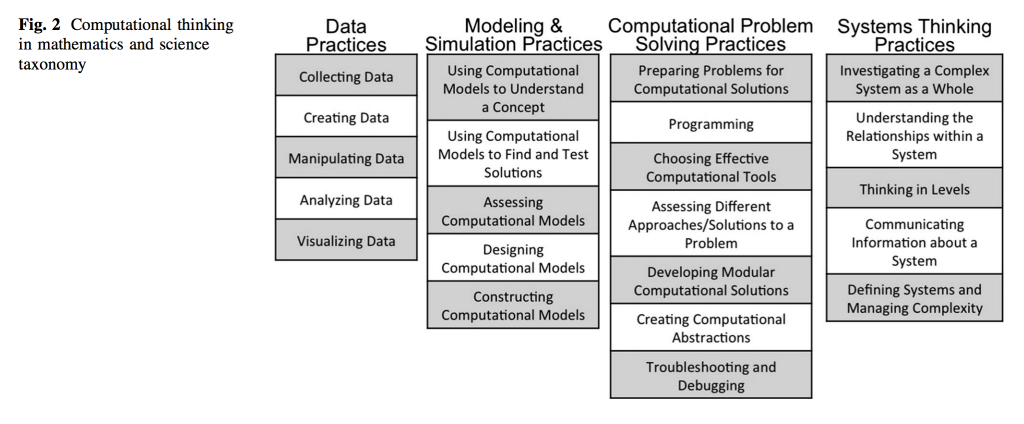
Dat is de titel van een artikel van Weintrop et al (2016) waarin ze een opzet geven voor het integreren van computational thinking (CT) in het wiskunde en science onderwijs. Een interessant artikel omdat dit een beeld geeft hoe je aandacht kunt besteden aan CT buiten het vakgebied computer science. De opzet die ze kiezen voor het integreren van CT is een taxonomie van doelen toegespitst op wiskunde en science. Op basis van eigen onderzoek komen ze uiteindelijk tot 4 categorieën: data practices, modeling and simulation practices, computational problem solving practices en system thinking practices. Belangrijkste reden voor de auteurs om CT te integreren binnen wiskunde en science is dat deze vakken daarmee beter aansluiten op de werkelijkheid van de wetenschap van nu. Daarnaast, geven de auteurs aan, kan het gebruik van computational tools en vaardigheden het begrip van wiskunde en science vergroten.
In het artikel gaan ze verder in op CT zelf, CT in K12 education, de steeds groter wordende rol van computation in wiskunde en science en de methode die ze gebruikt hebben om te komen tot hun taxonomie. Over de steeds groter wordende rol van computational methodes geven ze aan dat door de toegenomen rekenkracht steeds ingewikkeldere problemen kunnen worden opgelost, dat daardoor de wetenschap verandert en dat leerlingen daarop moeten worden voorbereid.
De Taxonomie
Zoals gezegd bestaat de taxonomie uit vier categorieën. Elke categorie is weer onderverdeeld in een aantal practices. Ik weet niet hoe practices zich het beste laat vertalen aangezien de auteurs zelf daar een apart punt van maken. In eerste instantie spreken ze over skills (vaardigheden) maar…
but concerns were raised, such as a request we move from the terms skills to the broader and more actionable practices to reinforce what it means to use these concepts as well as to reflect larger changes in the mathematics and science standards landscape.
Misschien dat werkwijze, praktijken of competenties een vertaling hiervoor zou kunnen zijn. Voor nu laat ik het maar even bij practices.
In het artikel lichten ze elke practice toe en daarna per practice alle onderdelen. Ik zal daarvan een korte samenvatting geven.
1. Data-practice
Data, zo geven de auteurs aan, is de kern van wetenschappelijk en wiskundige bezigheden. De manier waarop data wordt verzameld, gemaakt, geanalyseerd, gemanipuleerd en gevisualiseerd verandert snel. Leerlingen moeten leren dat data niet is geordend in structuren maar dat je die zelf nog moet aanbrengen.
1a. Collecting Data (dataverzamelen)
Door het observeren en meten kan data worden verzameld. Computational tools kunnen worden ingezet om data te verzamelen. Aan het eind van het artikel noemen de auteurs een voorbeeld van zo’n computational tool: De Tracker Video:
1b. Creating Data (Data maken)
Met behulp van computersimulaties kunnen wetenschappers data maken. Bijvoorbeeld om de evolutie van een melkwegstelsel te onderzoeken. Deze data is anders niet beschikbaar omdat dit soort processen bijvoorbeeld te lang zouden duren zonder simulaties.
1c. Manipulating Data (Data manipuleren)
Met data manipuleren wordt bedoeld het kunnen sorteren van data, filteren, opschonen, normaliseren en datasets kunnen samenvoegen. Hierbij moet ik denken aan het kunnen werken met Excel bijvoorbeeld. De auteurs noemen elders in het artikel nog tools zoals Tinkerplot, Fathom en SimCalc.
1d. Analyzing Data (Data analyseren)
Bij data analyseren gaat het er om dat je op zoek gaat naar patronen, afwijkingen, regels kunt definiëren om data te categoriseren, trends kunt vaststellen en verbanden kunt leggen. Nu er zoveel data beschikbaar is (big data) is het belangrijk dat je computational tools kunt gebruiken om de data te analyseren.
1e. Visualizing data (data visualiseren)
Computational tools kunnen helpen om data te visualiseren zodat je er ook met anderen over kunt praten. Denk hierbij aan diagrammen en grafieken. Maar ook aan dynamische, interactieve visualisaties.
2. Modeling and simulation practices (modellen en simulaties)
In de wetenschap is het maken, verfijnen en gebruik van modellen over fenomenen een belangrijk uitgangspunt. Je kunt hierbij denken aan stroomschema’s, diagrammen, vergelijkingen, chemische formules, computersimulaties en fysische modellen. Modellen kunnen worden gebruikt om te voorspellen hoe iets in de werkelijkheid zal gaan. De auteurs noemen hierbij specifiek niet statische representaties van fenomenen die gesimuleerd kunnen worden door de computer. Modellen maken het mogelijk om vragen te onderzoeken en hypotheses te testen die anders te duur, te gevaarlijk, te moeilijk of onmogelijk zijn uit te voeren.
2a. Using computational models to understand a concept (Computationele modellen gebruiken om een concept te begrijpen.
Een computational tool kan een goed leermiddel zijn om een concept te begrijpen zoals de afhankelijkheden in een ecosysteem en hoe objecten in een wrijfingsloze omgeving zich gedragen. Op zoek naar voorbeelden kwam ik op Wikipedia deze uitgebreide lijst tegen met computational models. Maar ik moest ook denken aan de GoLabs zoals Ton de Jong die beschrijft en de onderzoeken naar simulaties van Wouter van Joolingen met bijvoorbeeld SimSketch.
2b. Using computational models to find and test solutions (computational modellen gebruiken om oplossingen te vinden en testen)
Verschillende hypothesen testen zonder dat het teveel geld en tijd kost.
2c. Assessing computational models (computationals models beoordelen)
Hoe verhoudt het fenomeen zich tot de werkelijkheid? Welke abstracties zijn in het model ingebouwd? En welke invloed hebben de abstracties op de betrouwbaarheid van het model?
2d. Designing computational models (computational modellen ontwerpen)
Hierbij moeten technologische, methodologische en conceptuele beslissingen worden genomen. Hierbij gaat het om een ontwerpproces nog op papier.
2e. Constructing computational models (het construeren/ bouwen van computational modellen)
Hierbij gaat het echt om het bouwen van computational models. Hiervoor is programmeerkennis nodig.
3. Computational problem solving practice (computationeel probleemoplossend vermogen)
Het gaat hierbij om de toegepaste informatica die helpt om de wetenschap verder te helpen. Als leerlingen programmeren, algoritmes ontwikkelen en computationele abstracties maken kan dit een positief effect hebben op het bestuderen van wiskundige en wetenschappelijke fenomenen.
3.a Preparing problems for computational solutions (problemen zo formuleren dat ze computationeel kunnen worden opgelost)
Problemen lenen zich niet altijd automatisch om door een computerprogramma te worden opgelost. De kunst is om het probleem zo te formuleren dat het geschikt is om er met een computational tool mee aan de slag te gaan.
3b. Computer programming (programmeren)
Het gaat hierbij om het kunnen begrijpen van computerprogramma’s van anderen en zelf programma’s schrijven. Programmeerconcepten die hierbij belangrijk zijn: conditionele logica, iteratieve logica, herhaling, abstracties (waaronder subroutines en datastructuren). Niet iedereen hoeft een programmeur te worden, geven de auteurs aan, maar een basiskennis is wel belangrijk.
3c. Choosing effective computational tools (effectieve computationele middelen kiezen)
Het gaat hierbij om de vraag welk programma het beste past bij het probleem dat je hebt. Wat zijn de mogelijkheden en wat zijn de beperkingen?
3d. Assessing different approaches/ solutions to a problem (aanpakken en oplossingen beoordelen)
Als er meer mogelijkheden zijn om iets te doen dan is het belangrijk dat je de juiste keuze kunt maken. Je kunt denken aan de kosten, de tijd, duurzaamheid, herbruikbaarheid en flexibiliteit.
3e. Developing modular computational solutions (modulaire computationele oplossingen ontwikkelen)
Het gaat om het in stappen of stukjes op kunnen knippen van een proces. Zodanig dat ze gemakkelijk kunnen worden hergebruikt, voor andere doeleinden kunnen worden ingezet en fouten makkelijker kunnen worden opgespoord.
3f Creating computational abstractions (in staat zijn om abstracties te maken)
Vaststellen wat de hoofdlijnen zijn en wat de details. Dit helpt bij het schrijven van een computerprogramma, generaliseren, visualiseren van data en het vaststellen van de reikwijdte of schaal van een probleem.
3g. Troubleshooting and debugging (probleemoplossing en debuggen)
Bij het oplossen van problemen gaat het om het vaststellen van het probleem, het systematisch testen van het systeem om het probleem te isoleren en het reproduceren van het probleem om mogelijke oplossingen te testen.
4. System thinking practices (systeemdenken)
Er zijn problemen die je alleen op kunt lossen als je kijkt naar het systeem in het geheel en niet naar de afzonderlijke onderdelen. Systeemdenken is daarom een belangrijke vaardigheid. Voorbeelden van systemen die je in z’n geheel zou moeten bestuderen zijn natuurlijke selectie en populatieveranderingen in de natuur, het menselijk ademhalingssysteem en de algemene gaswetten. Ze benoemen daarbij ook de term cross-cutting concepts die ook al een keer was tegengekomen bij theorie over Wetenschap & Technologie. Computationele middelen kunnen een krachtig middel zijn om systemen te begrijpen.
4a. Investigating a complex system as a whole (een systeem als geheel bestuderen)
Soms is het effectiever om een systeem in het geheel te bestuderen in plaats van de afzonderlijke onderdelen. Dat betekent dat je sommige details moet kunnen weglaten. Computationele middelen zoals modellen en simulaties zijn hierbij handig om te gebruiken.
4b. Understanding the relationships within a system
Alhoewel het handig is om systemen als geheel te bestuderen is het ook handig om te weten hoe afzonderlijke onderdelen op elkaar reageren.
4c. Thinking in levels (in niveaus denken)
Het gaat hierbij om het kunnen onderscheiden van verschillende niveaus in een systeem en op basis daarvan onderzoek te doen.
4d. Communicating information about a system (communiceren over een systeem)
Als je een systeem onderzoekt is het de kunst om over de resultaten te kunnen communiceren. Visualisaties en infographics kunnen daarbij helpen. Belangrijk daarbij is de vraag wat je wel en niet presenteert.
4e. Defining systems en managing complexity (systemen definiëren en complexiteit managen)
Wat zijn de grenzen van het systeem dat je wilt gaan onderzoeken? Een systeem moet zo gedefinieerd zijn dat het bruikbaar is en productief.
De auteurs hebben een mooie opzet gemaakt waarin ze kijken hoe CT binnen wiskunde en science een rol kan spelen. Mijn idee is dat vooral science (onderzoekend leren) hierbij leidend is geweest. Ik heb tenminste het idee dat de opbouw zich als geheel vooral leent voor onderzoekend leren. De afzonderlijke onderdelen zouden naar mijn idee weer goed kunnen worden ingebed binnen rekenen-wiskunde. Rekenen-wiskunde is hierbij vooral een toepassing en niet zozeer het doel. In een volgende blogpost zal ik kijken of er op basis van bovenstaande ook vertalingen naar het basisonderwijs zijn te maken. En dan specifiek naar rekenen-wiskunde en wetenschap en technologie.
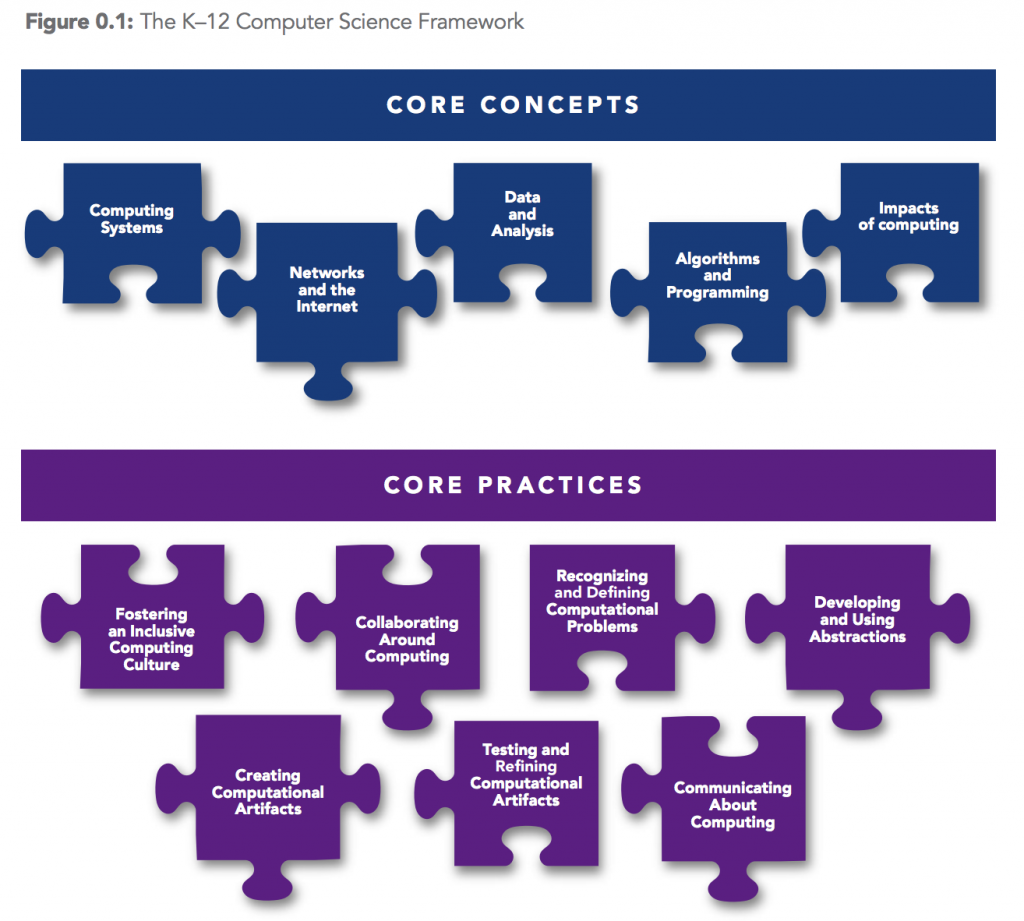
In het document K12 Computer Science Framework formuleren The Association for Computing Machinery, Code.org, Computer Science Teachers Association, Cyber Innovation Center, en National Math and Science Initiative de core concepts (kernconcepten) en core practices (kernpraktijken) van K12 Computer Science.
Computational Thinking maakt in hun overzicht deel uit van de core practices. Daarnaast hanteren ze nog crosscutting concepts. De uitleg daarvan is dat:
These “crosscutting concepts” provide thematic connections across the core concepts. The criteria for selection of a crosscutting concept was that it should
- apply across multiple core concepts,
- illuminate connections between different core concepts of computer science,
- build familiarity with fundamental themes in computer science through repetition in different
contexts, and - create a richer understanding of a concept statement in which it is integrated
De Crosscutting Concepts zijn:
1. Abstraction
2. System Relationships
3. Human–Computer Interaction
4. Privacy and Security
5. Communication and Coordination
Zoals gezegd maakt Computational Thinking dus deel uit van de core practices.
1. Fostering an Inclusive Computing Culture
2. Collaborating Around Computing
3. Recognizing and Defining Computational Problems
4. Developing and Using Abstractions
5. Creating Computational Artifacts
6. Testing and Refining Computational Artifacts
7. Communicating About Computing
Ze geven de volgende uitleg over waarom CT op deze manier in de core practices staat:
Computational thinking plays a key role in the computer science practices of the framework as it encompasses practices 3, 4, 5, and 6. Practices 1, 2, and 7 are independent, general practices in computer science that complement computational thinking. Multiple research articles and documents informed the delineation of computational thinking practices, such as Operational Definition of Computational Thinking for K–12 Education (ISTE & CSTA, 2011) and Assessment Design Patterns for Computational Thinking Practices in Secondary Computer Science (Bienkowski, Snow, Rutstein, & Grover, 2015).
Interessant vind ik ook dat ze schrijven dat ze nog niet in staat zijn om die core practices per niveau te omschrijven:
The practice statements delineate specific expectations by the end of 12th grade and are followed by a narrative that describes the progression leading to those end points. This structure differs from the grade-band delineation of the core concepts because the current research base and practitioner experience with practices in computer science do not provide enough information to create clear, grade-banded expectations. The narratives describe the practice progressions in a manner that is less prescriptive about developmental appropriateness to emphasize flexible expectations.
In mijn eerdere post van vandaag verwijs ik naar de CSTA-standaarden waar de SLO zich op baseert als het gaat om Computational Thinking (CT). Deze standaarden zijn in 2011 geformuleerd. CT is een onderdeel van computer science (CS) en CS bestaat naast CT uit: Collaboration, Computer Practice and Programming, Computer and Communication Devices, Community, Global and Ethical Impacts.
In het document van 2011 beschrijven ze het belang van CT als volgt:
We believe that computational thinking (CT) can be used across all disciplines to solve problems, design systems, create new knowledge, and improve understanding of the power and limitations of computing in the modern age. The study of computational thinking enables all students to better conceptualize, analyze, and solve complex problems by selecting and applying appropriate strategies and tools, both virtually and in the real world.
In het document van 2016, dat nog in conceptversie online staat wordt computational thinking niet meer als een apart onderdeel genoemd. De indeling die in dit document wordt aangehouden is: Computing Systems, Networks and the Internet, Algorithms and Programming, Data and Analysis, and Impacts of Computing.
Over computational thinking wordt in deze versie gezegd:
We believe that computational thinking is a problem solving methodology that expands
the realm of computer science into all disciplines, providing a distinct means of
analyzing and developing solutions to problems that can be solved computationally.
With its focus on abstraction, automation, and analysis, computational thinking is a
core element of the broader discipline of computer science and for that reason it is
interwoven through these computer science standards at all levels of K–12 learning.
CSTA kiest hier dus voor de lijn om CT te integreren in CS. Ben benieuwd hoe SLO en Kennisnet tegen deze verandering aankijken…